Le sextant en pratique

Dans le premier article dédié au sextant, on illustre la théorie du positionnement sur le globe par le sextant. Ce second article explique la mise en pratique du sextant.
D’abord on verra comment on réalise la mesure de la hauteur et de l’heure de cette dernière.
Ensuite on verra comment faire les calculs sans calculatrice avec les tables de Dieumegard et Bataille.
La mesure de hauteur
L’anatomie du sextant :
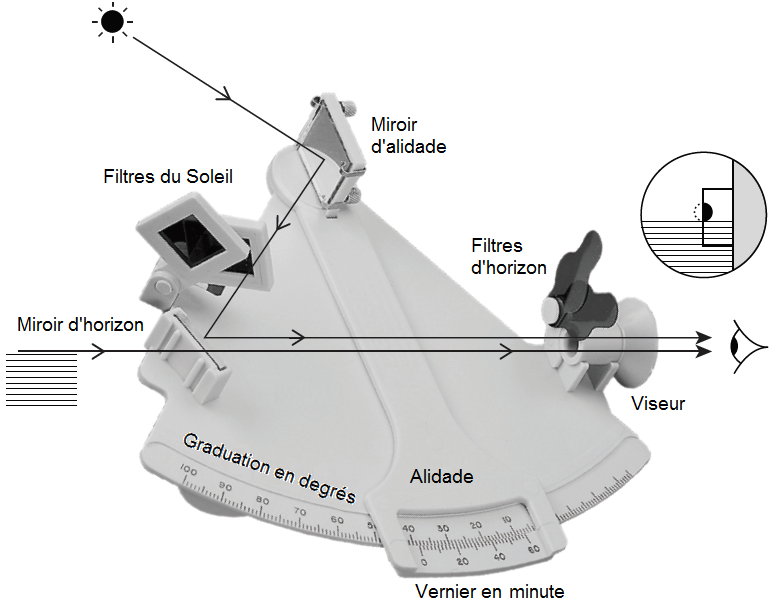
La manipulation du sextant demande un petit peu de pratique. Les quelques conseils de la vidéo de Navastro, vous ferons gagner du temps
Les 10 étapes de la mesure de hauteur :
- Enclenchez le chrono à une minute finie de l’heure TU
- Notez l’heure TU à cet enclenchement
- Allez dehors pour mesurer la collimation de son sextant sur l’horizon
- Notez cette collimation
- Placez tous les filtres de protection du sextant
- Visez le Soleil avec le sextant
- Gardez le Soleil dans le viseur tout en basculant le sextant vers le bas et en poussant l’alidade
- Si la mer ne réfléchis pas trop le Soleil, vous pouvez relever les filtres d’horizon
- Ajustez l’alidade pour placer le bord inférieur du Soleil sur la ligne d’horizon
- Quand le Soleil colle à la ligne d’horizon, arrêtez le chrono
Voilà la mesure est terminée. Il ne vous reste plus que à noter la mesure du sextant et du chrono.
Il faudra sommer la mesure du chrono avec son heure d’enclenchement pour avoir l’heure de la mesure.
On retira la valeur de collimation de la mesure du sextant.
Les erreurs de mesures
La mesure brut du sextant comportant des erreurs, il faut corriger la valeur mesurée. On appelle la mesure brut Hi comme Hauteur instrumentale et la mesure corrigée Hv comme Hauteur vraie.
On considère 4 erreurs de mesure lors de notre visée au sextant :
- L’erreur de collimation
- L’erreur dû à l’élévation de l’oeil au-dessus de la mer
- L’erreur dû à la réfraction du Soleil dans l’atmosphère
- L’erreur dû à la prise du bord inférieur du Soleil
La collimation est expliqué dans la vidéo de Navastro ci-dessus.
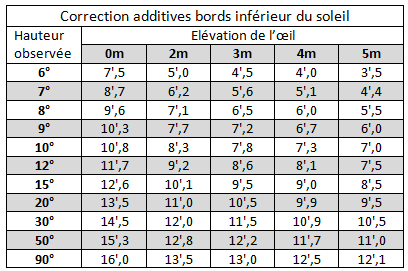
Les valeurs des erreurs 2. 3. et 4. sont additionnées et répertoriées dans le tableau ci-dessous.
1. La collimation
La collimation est l’erreur du sextant que l’on connait en la mesurant avant chaque visée. Voir la vidéo précédente de Navastro.
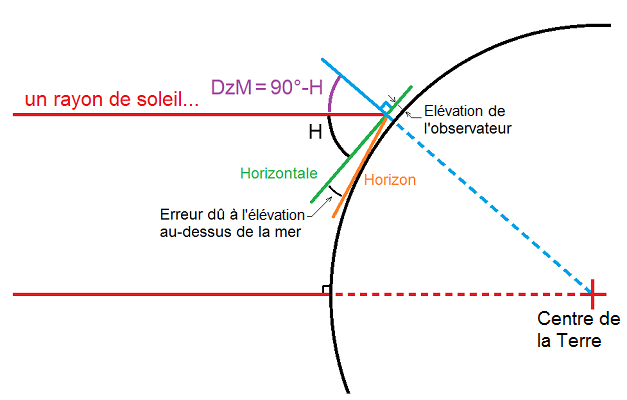
2. Elévation de la visée
L’erreur dû à l’élévation de la visée au-dessus de la mer est connue en fonction de l’altitude de notre œil de visée.
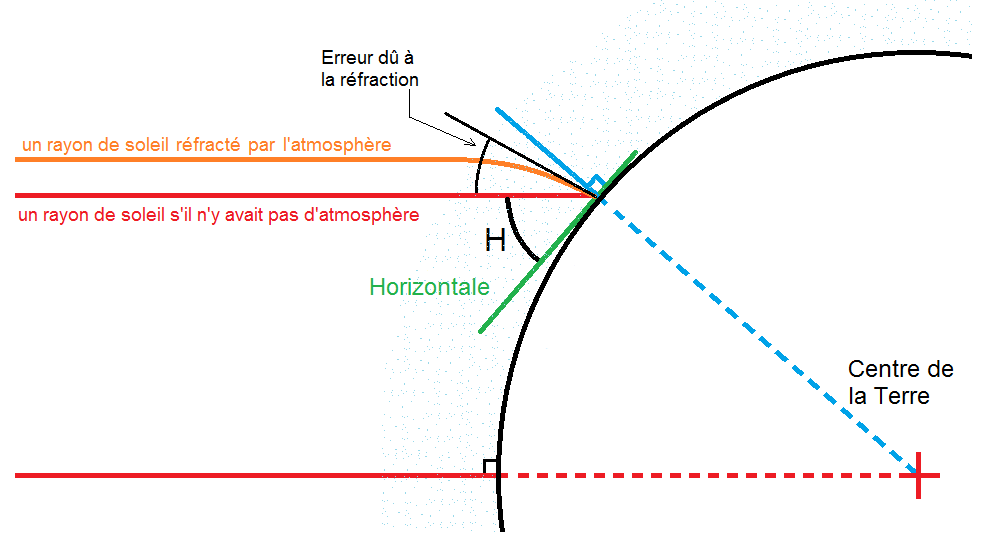
3. La réfraction de l’atmosphère
L’erreur de réfraction est connue en fonction de la hauteur du Soleil.
4. La visée au bord inférieur
Dans l’idéal notre mesure devrait se faire en posant le centre du Soleil sur l’horizon. Mais il est plus précis de poser le bord inférieur sur la ligne d’horizon. On corrige ensuite l’angle mesuré d’un 1/2 diamètre.
A. Calcul pour la 1ère droite des hauteurs
Donc dans l’article précédent, on vu la théorie, que l’on peut appliquer à la calculette.
Mais à bord d’un bateau il n’y a parfois pas de calculette et il existe donc des méthodes pour tracer les droites de hauteur sans chinoiseries d’électroniques.
Parmi ces méthodes à l’ancienne, il y a les tables de Dieumegard et Bataille. Ces tables permettent de faire les calculs à l’aide des propriétés du logarithme. Ainsi au lieu de multiplier entre eux les cosinus et autres sinus, on va additionner leurs logarithmes.
Repartons de notre exemple :
Nous rentrons du Fastnet et arrivons en mer d’Iroise le 11 mai 2020, il fait beau et décidons d’en profiter pour faire une droite de hauteur. Il est exactement du 12H34 et 18 secondes quand nous mesurons la hauteur du Soleil à 52°54’. On utilisera le même point de calcul avec L=48°,10’ N et G=+5° O.
Pour utiliser les tables de Dieumegard et Bataille, on remplit un canevas distribué par le site navastro.fr. L’utilisation de ce canevas va nous permettre de calculer à la main l’intercept I et l’azimut Z pour une droite de hauteur. Lien de téléchargement du canevas vierge
Je vous présente le canevas remplis de la 1ere droite des hauteurs accompagné des infos à aller chercher dans chacune des tables de Dieumegard et Bataille.
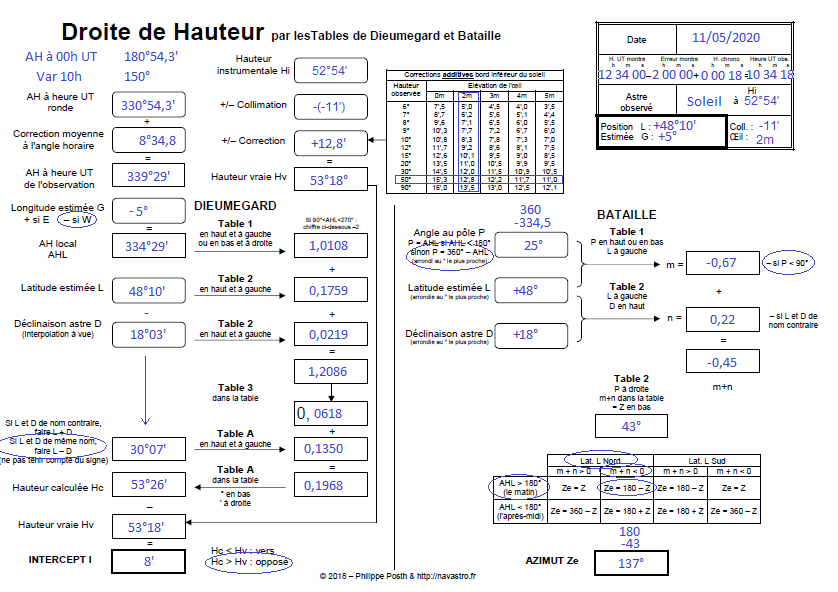
Ouvrir le canevas rempli dans un nouvel onglet
Données de la mesure, encart en haut en droite
Cet encart est la première chose à remplir. On inscrit la date. On réalise le calcul de l’heure exacte de notre mesure en tenant compte du décalage horaire de notre heure locale et de la mesure du chrono. On y inscrit notre valeur de la hauteur instrumentale Hi qui correspond à la mesure brute du sextant. Puis on ajoute nos choix de coordonnée L et G du point d’estime Pe.
2.Hauteur vraie Hv
On soustrait la collimation du sextant. Elle est ici de -11′.
On utilise les données du tableau de corrections additives au bord inférieur du soleil. Ce canevas s’applique donc pour des mesures au sextant de la hauteur entre l’horizon et le bord inférieur du Soleil. Notre hauteur mesurée est proche de 50°. On entre par la ligne 50°. On estime notre altitude au-dessus de la mer à 2m. On prend la colonne 2m. On retrouve la valeur de 12,8’ que l’on arrondie à 13′. On additionne 13′ à notre hauteur instrumentale pour calculer la hauteur vraie.
\fbox{Hv=52°54'+11'+13'=53°18’}\:
3. Angle Horaire
On prend l’angle horaire vrai à 00H00 le 11 mai 2020 AHvo par dans les éphémérides.
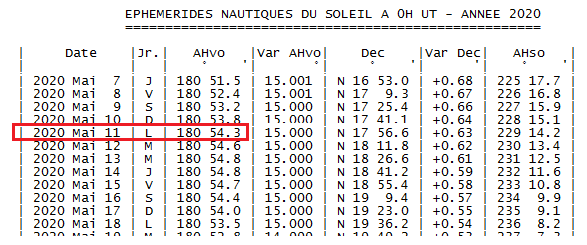
AHvo=180° 54,3'\:
On regarde la table angle horaire.
On prend la valeur en degrés correspondant à l’heure UT de la mesure, ici 10h donc on récupère l’angle de 150°.

On ajoute l’angle de 150° à AHvo soit :
AH\: à\: UT\: à\: l' heure\: ronde=180°54,3'+150°=330°54,3'\:
On reprend la table angle horaire pour récupérer la correction moyenne à l’angle horaire. Après 10h le temps écoulé jusqu’à la mesure est 34 minutes et 18 secondes. On entre dans la colonne 34 et la ligne 18 pour récupérer l’angle 8°34,5′.
Correction\: moyenne\: à\: l’angle\: horaire=8°34,5’\:
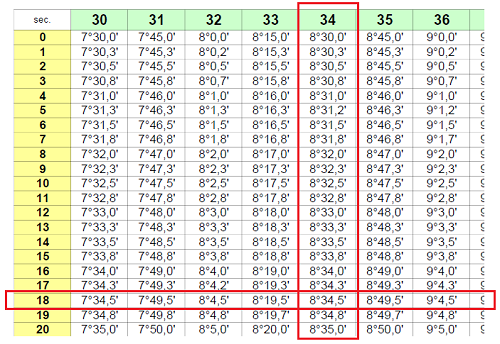
On additionne 330°54,3’ et 8°34,5’ arrondi à la minute près pour obtenir AH.
\fbox{AH = 330°54,3’ + 8°34,5’=339°29,1’=339°29’}\:
5. Angle Horaire Locale
On reporte notre longitude G dans la case longitude estimée.
On prend soins de lui appliquer le signe adéquat. Ici on lui met le signe négatif puisqu’il s’agit d’une longitude Ouest.
On fait le calcul pour remplir la case de l’angle horaire local AHl.
\fbox{AHl=339°29'\:-5°=334°29'\:}\:
6. Latitude et déclinaison
On inscrit la latitude L dans la case correspondante.
L = 48°10'\:
On réalise une interpolation à vue de la déclinaison pour notre heure de mesure à partir des éphémérides.
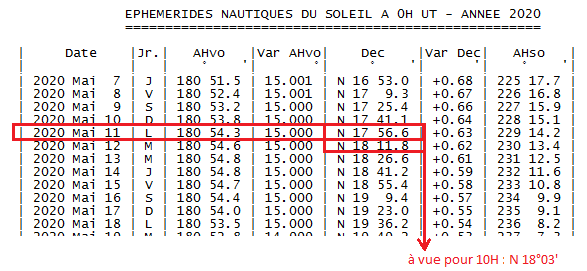
D=Dec+ 10h34’18″ \times Var Dec \:
D \approx 17°57'+ 10h \times 0,6 \:
D \approx 17° (57 + 10 \times 0,6) '\:
D \approx 17° 63'\:
\fbox{D = 18° 03'\:}
Puis on remplis la case sous celles de L et D en faisant ici la soustraction car L et D sont de même nom. En effet, L est une latitude Nord et D est une latitude Nord aussi.
\fbox{48°10'\:-18°03'=30°07'\:}
7. Dieumegard Table 1
On prend l’angle horaire local AHl pour rentrer dans la Table 1.
Si AHl est compris entre 0° et 180° : en haut pour le nombre de degrés et à gauche pour les minutes.
Si AHl est compris entre 180° et 360° : en bas pour le nombre de degrés et à droite pour les minutes (notre cas ici).
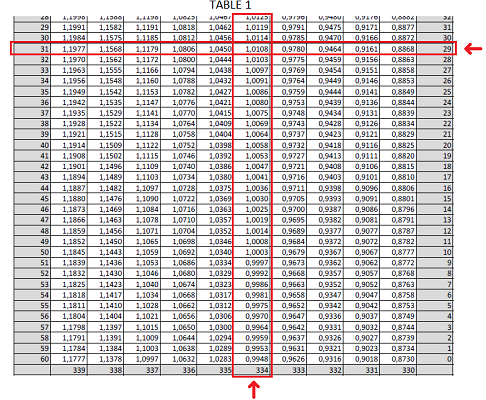
On récupère le nombre :
\fbox{1,0108} .
Qui est en fait égal à :
-\log \left( 1-\cos(334° 29'\:) \right)
8. Dieumegard Table 2
8.1 Latitude estimée
On prend la latitude estimée L pour rentrer dans la Table 2.
En haut pour le nombre de degrés et à gauche pour les minutes.
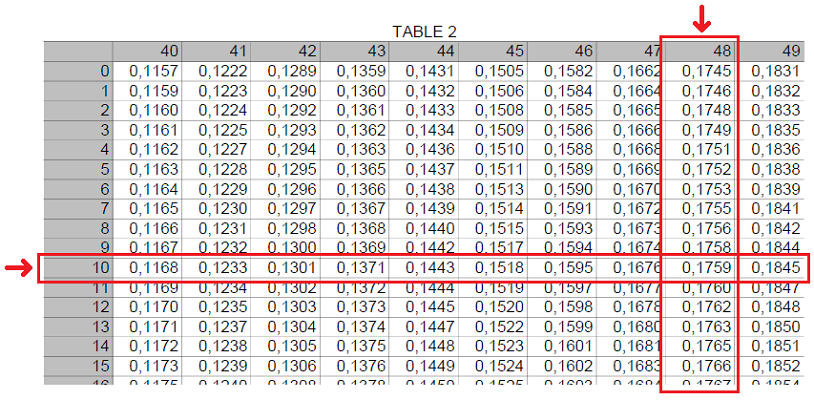
On récupère le nombre :
\fbox{0,1759} .
Qui est en fait égal à :
-\log \left( \cos(48° 10'\:) \right)
8.2 Déclinaison
On fait la même chose avec la déclinaison D qu’avec la latitude.
On prend la déclinaison D pour rentrer dans la Table 2.
En haut pour le nombre de degrés et à gauche pour les minutes.
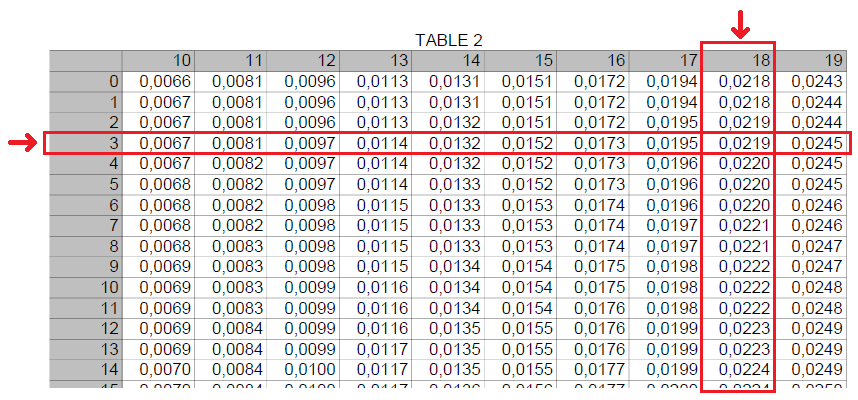
On récupère le nombre :
\fbox{0,0219} .
Qui est en fait égal à :
-\log \left( \cos(18° 3'\:) \right) .
9. Dieumegard Table 3
On fait la somme des trois nombres récupérés précédemment dans les Tables 1 et 2.
1,0108+0,1759+0,0219= \fbox{1,2086}
On prend cette somme pour rentrer dans la Table 3.
On recherche 1,2086 parmi les nombres dans le tableau.
On récupère le nombre de la colonne correspondante pour les deux premiers chiffres après la virgule.
On récupère le nombre de la ligne correspondante pour le 3ème et 4ème chiffres après la virgule.
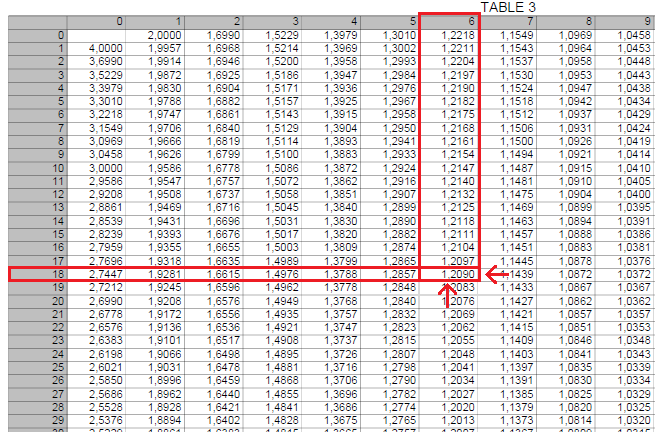
On récupère le nombre :
\fbox{0,0618}
Qui est en fait égal à :
10^{-1,2090} .
10. Dieumegard Table A
On rentre dans la Table A avec le résultat de L-D, soit 30°7′.
En haut pour le nombre de degrés et à gauche pour les minutes.
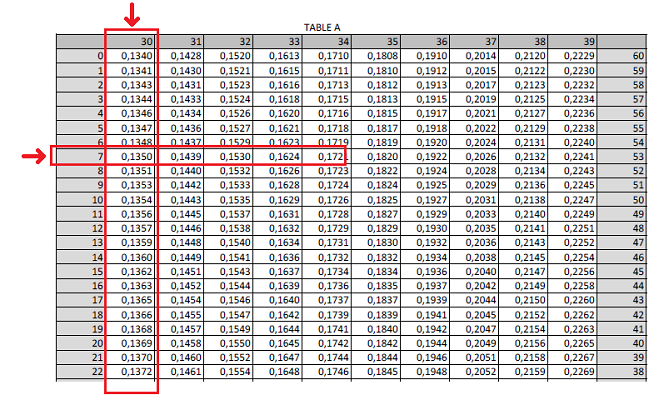
On récupère le nombre :
\fbox{0,1350}
Qui est en fait égual à :
1-\cos(30°7'\:) .
On additionne ce nombre avec le résultat de la Table 3.
0,0618+0,1350=\fbox{0,1968} .
On rentre avec cette somme dans Table A.
On recherche 0,1968 parmi les nombres présents dans le tableau.
On récupère le nombre de degrés en bas et les nombre de minutes à droite.
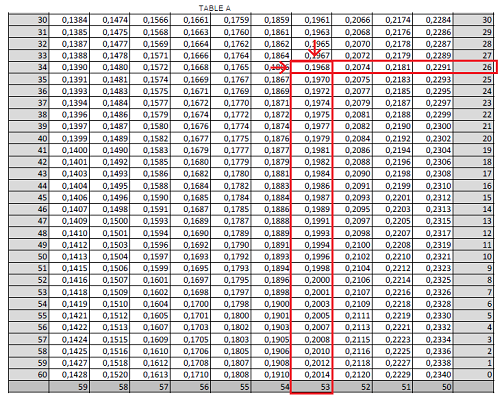
On récupère l’angle :
\fbox{53°26'\:}
Qui est en fait égal à :
\arcsin(1-0,1968) .
On reporte cet angle dans la case correspondante à Hc.
11. Intercept
Il ne nous reste plus qu’à soustraire Hv à Hc pour obtenir l’intercept.
53°26'\: - 53°18'\: = \fbox{8'\:}
12. Bataille Table 1
Maintenant que l’on a calculé l’intercept, on va calculer l’azimut Z avec les tables de Bataille. A noter que l’on n’aura pas besoin d’être précis à la minute d’angle près comme il faut l’être pour le calcul de l’intercept. On se contentera ici d’être précis au degré près.
Nous sommes dans le cas où AHl > 180°, donc on inscrit le résultat de 360-AHl dans la première case.
360°\: - 334,5°\: \approx \fbox{25°\:}
On reporte la latitude estimée L au degrés près dans la case d’en-dessous.
On rentre avec P=25° et L=48° dans le table 1. P en haut et L en gauche.
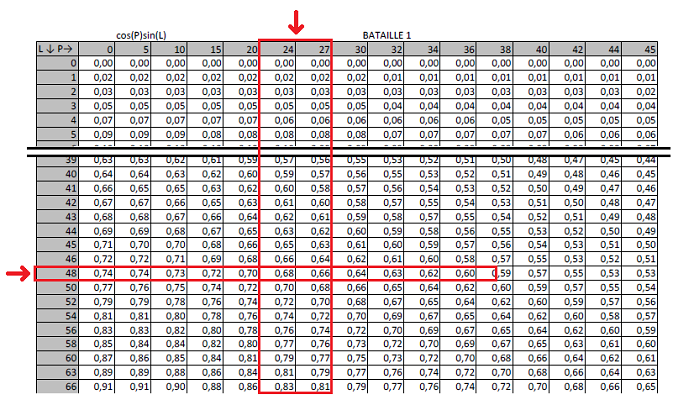
On obtient 0,67 auquel on rajoute devant un signe négatif parce que P<90°.
\fbox{m=-0,67\:}
13. Bataille Table 2
On reporte la déclinaison D dans la 3ème case d’entrée du calcul de Bataille.
On rentre avec L=48° et D=18° dans la table 2. D en haut et L à gauche.
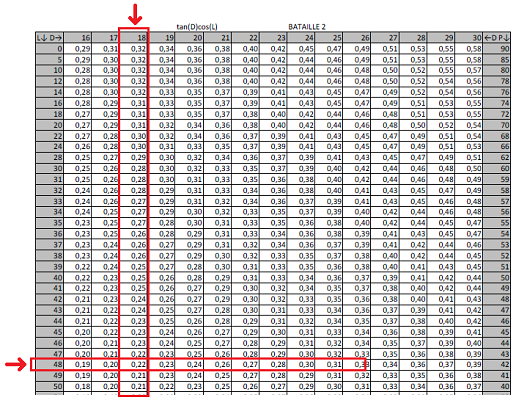
On obtient 0,22. On laisse ce nombre positif parce que L et D sont de même nom.
\fbox{n=0,22\:}
On additionne m et n.
m+n=\fbox{-0,45\:}
On rerentre dans la table 2 avec 0,45. On cherche -0,45 dans la table 2 pour la ligne correspondant à P=25°. P est noté à droite.
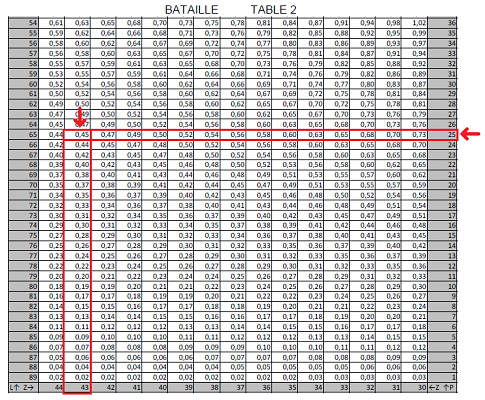
On obtient Z en bas.
\fbox{Z=43°\:}
Il ne reste plus qu’à appliquer les critères de correction du dernier tableau.
On est dans le cas où :
- AHl > 180°
- la latitude estimée L est Nord
- m+n < 0
Donc on fait 180-Z pour obtenir l’azimut Ze
Ze=180°-Z= \fbox{137°\:}
14. Tracé sur carte de la droite de hauteur
C’est bon ! On a notre intercept I et et notre azimut Ze pour tracer la première droite de hauteur.
Se reporter à la fin de l’article « Comment se repérer avec un sextant » pour comprendre comment tracer une droite de hauteur.
B. Deuxième droite des hauteurs
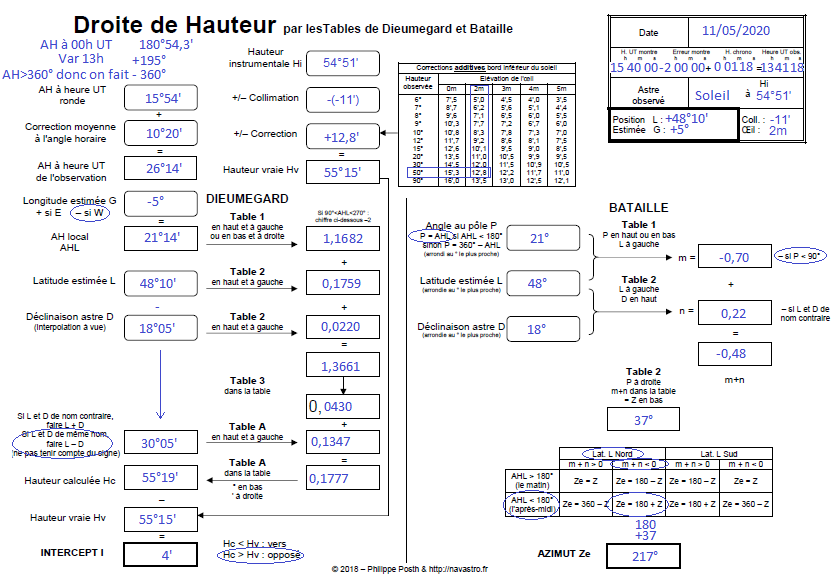
Je vous propose aussi ce deuxième canevas rempli de Dieumegard et Bataille sur la base du calcul de la deuxième droite de hauteur.
Toutes corrections faites sur notre mesure, on relève la hauteur du Soleil à 55°15’ à exactement 13h41 et 18 secondes UT.
On gardera la même position estimée, soit Pe a pour coordonnées 48°10’N et 5°W donc L =+ 48°10’ N et G=+5° O.
Bonsoir Hugo, je te remercie pour ce travail colossale mais très compliqué , si tu as aussi la formule de l’aspirine je suis preneur, en te souhaitant bon vent je vais aller bosser tout cela.
En vous remerciant pour ce doc très complet , toutes mes félicitations et en vous souhaitant bonne chance pour vos projets. respectueusement Fred.
Merci beaucoup Fred ! J’ai essayé de rendre cette pratique un peu plus accessibles.
Amicalement,
Hugo
Bonjour Hugo,
Félicitations ! C’est la première fois que je vois le détail des calculs… Le sextant est un appareil qui me fascine ! J’imagine que la mer doit être très calme pour pouvoir faire des mesures avec une précision de l’ordre de la minute d’angle, debout sur le pont et tenant le sextant à bout de bras comme le capitaine Haddock ! Est-ce que tous les marins qui ont utilisé le sextant avant l’ère des gps faisaient tous ces calculs compliqués pour déterminer leur position ? Cordialement, Marc
Bonjour Marc,
Oui c’était la méthode officielle enseignée dans la Marine avant l’avènement du GPS. Je crois qu’elle est d’ailleurs toujours enseignée pour se repérer en cas de perte de l’électronique du bord.
Merci pour ton commentaire,
Bon vent !
Hugo
Merci Hugo
Super boulot
Bonne mer
Jacques