Se repérer au sextant ?

Alors en fait, pour se repérer en mer, nos aïeux utilisaient cette technique pour ne pas trop se louper de port d’arrivée quand ils traversaient les océans les cales remplies d’esclaves ou autres cargaisons précieuses. Cet instrument était plutôt utile parce qu’avant les mecs se gouraient carrément de continent ! RIP Señor Colomb si tu nous entends…

Ensuite nos parents ont utilisé la gonio pour se positionner. En gros, imaginez que votre poste radio puisse connaitre la direction de l’antenne qui émet votre Jeu des 1000 francs préféré. Et attention, encore un petit effort, imaginez qu’il puisse aussi connaitre la direction de l’antenne qui émet les Grosses Têtes (votre 2ème émission préf). Vous tracez ces deux droites sur la carte des antennes radios de France que personnes n’a chez soi, et bien Mesdames Messieurs devant vos yeux ébahis : vous êtes à l’intersection des deux droites ! Waouh ! En fait en mer vous remplacez vos émissions radio préfs par des bulletins dédiés au positionnement au son atroce, les antennes sont sur les phares et la carte des antennes radios de France est une carte marine que tout le monde a à son bord. Waouh ! A noter que ce moyen de positionnement est beaucoup utilisé dans l’aviation.

Même si dans le secteur de l’aviation, il est maintenant aussi largement détrôné par un système disponible partout dans le monde avec une précision au mètre près. Vous ne voyez pas quel est ce truc super ? Mais si, tu sais là, le machin qui te place direct sur une carte sans connexion internet… Même qu’il faut envoyer des trucs avec panneaux solaires en orbite autour de la terre pour que ça marche et tout… Mais si avec un acronyme qui voudrait dire que c’est un système qui te positionne partout dans le monde mais en anglais… Du genre Global Positioning System… Oui c’est ça le GPS ! Effectivement le GPS est arrivé dans le game grâce à l’armée américaine et comme a l’habitude de faire cette dernière, ce système de positionnement a tout pété. C’est l’un système des plus fiable au monde. A part si vous vous trouvez dans le tunnel de l’A86 ou au fond de la fosse des Mariannes, il vous donnera vos coordonnés géographiques à la dixième de seconde près (je parle d’angle là quand je parle de seconde, ouais je vous chauffe pour la suite), reste à reporter ces coordonnées sur une carte fiable, mais ça ce n’est plus un problème de positionnement à proprement parlé. Pour le fonctionnement du GPS, il ressemble à celui de la gonio vu plus haut (bande de ouf c’est pas moi qui vais réécrire, c’est vous qui allez relire) sauf qu’on ne mesure pas la direction mais la distance et que l’on a besoin de 4 satellites et plus juste 2 parce que l’altitude et le temps viennent se rajouter à l’équation de positionnement.

Bon voilà en gros pour les techniques de positionnement qui ont parcouru les âges. Si vous en avez déjà marre et vous vous êtes dit « mais putain quand est ce qu’il va nous expliquer comment utiliser cette saloperie de sextant », prenez juste le temps après la présentation des systèmes de positionnement plus récents de vous demander qu’est ce qui vous pousse vraiment à utiliser ce truc archaïque.

Inspirez profondément et imaginez-vous perdu sur cet océan bleu. Dans le coffre à tribord vous avez votre sextant, un chrono, des tas de papiers et un crayon alors dans le coffre à bâbord vous avez juste votre tablette tactile avec Navionics installé dessus. Maintenant expirez profondément et prenez votre décision : coffre tribord ou coffre bâbord ? Ça y est vous avez choisi ?

Ok si vous êtes encore là c’est que vous aussi vous faîtes partie de ces gens un peu chiant qui prennent un malin plaisir à tout comprendre quitte à se faire s’emmerder 1 heure sur des mesures et des calculs que font très bien les ordis. Vous kiffez en baver quand c’est inutile (oh mon dieu me dite pas que vous aussi vous faites du Mini 6.50 ?) et encore plus si c’est pour laisser de côté tout ce qui est électronique et autres chinoiseries pour régler ce problème de position à la mano ! Sans intermédiaire ! C’est entre vous et lui maintenant ! On y va ! On y croit !

I. Le fonctionnement expliqué avec les mains

Alors première à chose à comprendre : la théorie générale du positionnement par le sextant avec le soleil. Ce n’est pas trop compliqué alors si je n’arrive pas à vous expliquer ça, c’est mort pour la suite parce que la pratique est beaucoup plus compliquée.

A. Les éphémérides

Il faut savoir qu’il y a des mecs très intelligents qui ont calculé en tout instant la positon du Soleil par rapport à la Terre. Un peu comme pour les marées, tout est rangé dans des grands tableaux que l’on appelle éphémérides, du Soleil en l’occurrence. En fait, ce n’est pas la position du Soleil à proprement parlé qui est reportée dans les éphémérides, mais le lieu à la surface du globe qui est sous le soleil exactement, comme dit Gainsbourg. C’est le lieu qui est pile à l’endroit où le Soleil frappe à la verticale. On appelle ce lieu le pied du Soleil. Le pied du Soleil se déplace entre le tropique du Cancer et du Capricorne en faisant un tour du globe chaque jour (ben oui forcément c’est même comme ça qu’on compte les jours).

Télécharger les éphémérides

On verra plus tard comment lire les éphémérides mais elles sont là et maintenant peut connaitre le lieu à la verticale au soleil tout le temps.

B. La Hauteur du Soleil

Maintenant, utilisons le sextant pour mesurer de l’angle entre le soleil et l’horizon. On va l’appeler la hauteur H du Soleil. Alors déjà vous voyez, il y a truc étrange, dès qu’on parle de sextant, on appelle les angles comme des distances ! On pourrait croire que l’on mélange les conserves avec les boites de gelcoat mais en fait pas du tout. Avec le sextant, les distances sont des angles et l’inverse aussi.

H=Hauteur=angle\:mesuré\:avec\:le\:sextant\:entre\:l'horizon\:et\:le\:Soleil

C. Les angles c’est des distances

Mais pourquoi Jamy ? Hé bien, toi qui connais les cartes marine, tu n’es pas sans savoir que le mille nautique est défini comme étant une minute d’un degré d’angle en latitude. Une minute de degré est en fait un 60^ème de degrés. Et la latitude est l’angle entre l’équateur et une position donnée. Donc si on convertit notre latitude en mille nautique, on obtient la distance qui nous sépare de l’équateur. Pour faire cette conversion on multiplie par 60 de nombre de degrés. Par exemple, en rade de Brest la latitude est approximativement de 48°20’ Nord donc en rade de Brest on se trouve à 48°20’ de l’équateur ou 48×60+20=2900 milles de l’équateur. D’où le numéro de département qui est 29. Non ça c’est une coïncidence. Bon l’équateur c’est flou parce que c’est une droite et du coup il y a plein de point dessus. Mais vous connaissez le complémentaire ? C’est 90° moins l’angle. Et ben du coup le complémentaire de notre latitude c’est la distance qui nous sépare du pôle Nord. Donc avec la rade de Brest, ça fait 90°-48°20’=41°40’=41×60+40=2500 milles. Et là tu comprends qu’en rade de Brest on est plus près du Pôle Nord que de l’équateur.

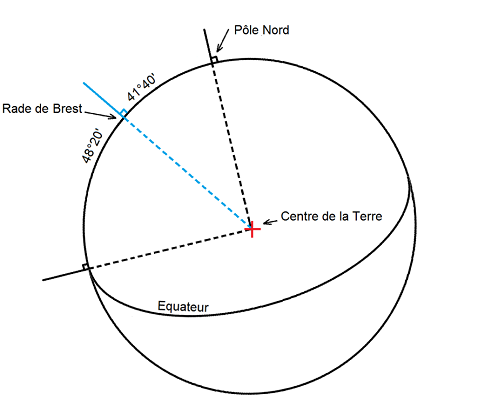
Mais au-delà de l’histoire de Brest qui est plus proche du Pôle Nord que de l’équateur, ce qui est important de comprendre c’est qu’entre deux points quelconques du globe, la distance qui les sépare est l’angle entre les deux verticales des lieux. On appelle cet angle la distance zénithale. Pour s’en rappeler on peut se dire que la distance zénithale est l’angle entre deux droites zénithales. C’est la première chose importante à capter pour le sextant.

Et la deuxième chose importante c’est que : les distances c’est des angles et les angles c’est des distances ! Ce n’est pas français pour faire un effet mémoire.

D. La distance au Soleil DzM

Ok mais alors dans le cas de l’angle H entre l’horizon et le Soleil, elle est où la distance là ? Bonne question Fred ! Alors regardons ce schéma avec l’angle de la hauteur H représenté :

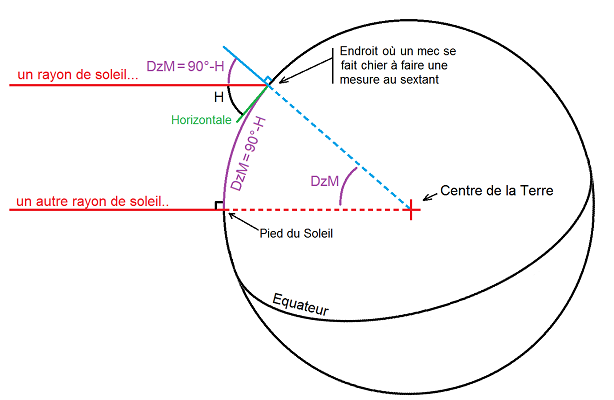
Et voilà sous vos yeux ébahis le complémentaire de la hauteur H se retrouve bien être une distance : celle qui sépare le lieu de mesure et la verticale du Soleil. Le complémentaire de la hauteur se trouve être la distance entre le pied du Soleil et le lieu de mesure. Les deux rayons de Soleil sont parallèle. Le complémentaire de la hauteur se retrouvent au lieu de mesure et au centre de la Terre.

C’est donc à ça que va nous servir le sextant : mesurer notre distance à la verticale du Soleil, connu par les éphémérides. On va appeler cette distance DzM comme Distance zénithale Mesurée.

DzM=90°-H=Distance\:zénithale\:Mesurée =Distance\:entre\:moi\:et\:et\:le\:lieu\:où\:le\:Soleil\:est\:à\:la\:verticale

On appellera Ps le pied du Soleil.

Ps=Point\:Soleil =Lieu\:où\:le\:Soleil\:est\:à\:la\:verticale\:connu\:par\:les\:éphémérides

E. Le cercle de hauteur

On trace sur le globe l’immense cercle de centre Ps et de rayon DzM (Distance zénithale Mesurée). On appellera ce cercle, le cercle de hauteur puisqu’il représente l’ensemble des positions qui ont la même mesure de hauteur du Soleil.

Pour véritablement avoir notre position, il faudra faire deux mesures au moins. Une technique qui a l’avantage de n’utiliser que le Soleil est de refaire cet exercice quand le Soleil a tourné de plus 60°, soit 3-4h plus tard, pour obtenir un deuxième cercle de hauteur. On décale le premier cercle en suivant le trajet estimé par notre bateau entre les deux relevés. On obtient notre position à l’intersection du second cercle (vert ci-dessous) avec le premier cercle décalé (rouge ci-dessous).

II. Application sur la carte marine

C’est bon j’ai perdu personne ? Parce que moi j’ai l’impression que c’était la partie facile.

A. Problème de tracé

Cet exercice qui parait limpide à l’échelle du globe est en pratique impossible à mettre en œuvre dans un voilier. Comment dessiner ces cercles immenses sur la petite représentation d’une portion de globe qui est ta carte marine ? Même avec une carte 1:100 000 il faudrait un énorme compas. Et puis une grande carte qui comprenne le point Ps et notre lieu de mesure. Impossible ! Alors un mec dans la Marine Nationale au 19^ème je crois a eu une idée pour simplifier le problème. Enfin pas pour le simplifier mais pour le résoudre, parce qu’en ça le complique en réalité. Et c’est là que selon moi il faut s’accrocher un peu aux explications…

B. Solution avec la droite de hauteur et la position estimée

Voilà ce que ce milouf, s’est dit : je sais qu’une partie du cercle passe dans ma carte, ou alors c’est que je me goure complétement de carte. Alors je vais calculer la distance à Ps avec un point au pif de ma carte. Normalement, je ne devrais pas être loin de DzM et au pire je reporte l’écart sur la carte.

Ok donc on va expliquer ça. Le point au pif, appelons-le Pe comme Point d’estime. Voilà le schéma :

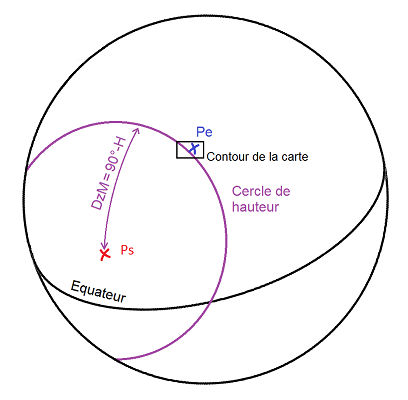
A l’échelle de la carte ça donne ça :

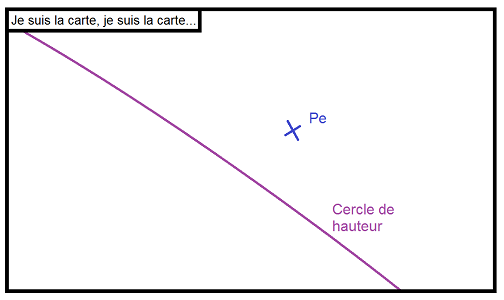
Sauf qu’en fait on n’arrive pas à tracer le cercle de hauteur parce qu’il est trop grand par rapport à la carte. Mais on connait son rayon (DzM=90°-H) et son centre (Ps).  En fait, au début, la carte ressemble à ça :

Maintenant on va faire deux calculs :

1. Calcul de la distance entre Ps et Pe que l’on appellera DzC comme distance zénithale calculée.
2. Calcul de l’azimut de Ps depuis Pe que l’on appellera Z

Avec ces résultats voilà ce qu’on va pouvoir tracer :

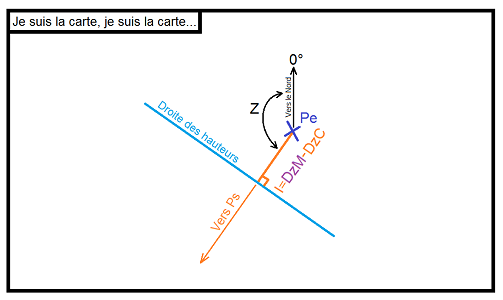
On utilise l’angle Z et la différence entre les distances DzC et DzM pour tracer une droite de hauteur qui contient notre position. La droite de hauteur s’appelle ainsi puisqu’elle contient toutes les positions à partir desquels on mesure la même hauteur H (DzM = 90°-H). La droite de hauteur sera notre sacre saint résultat de toutes nos mesures et calculs. Vous me direz : oui mais la droite de hauteur est une droite et nous on voulait un arc de cercle ! Ouai bah osef, ce sera une droite parce que c’est plus simple. Et que franchement l’arc de cercle à l’échelle de la carte… franchement on dirait une droite.

On nommera intercept,  la différence entre DzM et DzC que l’on notera I.

I=Intercept=DzM-DzC

Mais pour en revenir au choix de la position de Pe du début, imaginer que l’on ait choisi un autre Pe, on aurait calculé une autre valeur de la distance DzC entre Pe et Ps et un autre angle Z entre Pe et Ps. En fait ces calculs différents nous aurait conduit à tracer la même droite de hauteur.  

C. Calcul de DzC et Z

Bon passons aux calculs justement pour en arriver à Z et DzC.

1. Le triangle de calcul

Il va falloir un troisième point pour faire ce calcul. On va prendre le Pôle Nord ce qui va créer un triangle avec Pe et Ps.

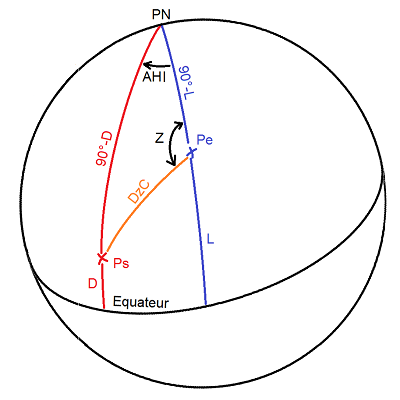
La déclinaison du Soleil est nommée D. D est aussi la latitude de Ps. La latitude de Pe est nommée L.

2. L’angle horaire et l’angle horaire locale

L’angle AHl est l’Angle Horaire local. AHl est l’angle formé au Pôle Nord entre les directions de Ps et de Pe.

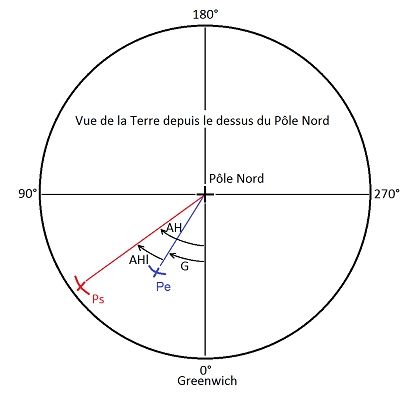
On calcule AHl comme étant l’écart entre la longitude de Ps et de Pe. On appelle G la longitude de Pe. Pour s’en rappeler on peut se dire que Pe est éloigné de l’angle G du méridien de Greenwich. On appelle AH la longitude de Ps. AH signifie juste Angle Horaire par opposition à AHl pour l’Angle Horaire local. AH est l’angle horaire de référence. Il est pris à partir du méridien du Greenwich.

AHl=AH-G

Les angles horaire AH et AHl sont des nombres compris entre 0 et 360°. Si la soustraction de AH par G donne un résultat supérieur à 360°, on retire 360°. Si, par ailleurs, la soustraction de AH par G donne un résultat négatif, on ajoute 360°. Le matin correspond des angles AHl compris entre 180° et 360° et l’après-midi correspond à des angles horaires local compris entre 0° et 180°.

3. Récapitulatif des grandeurs

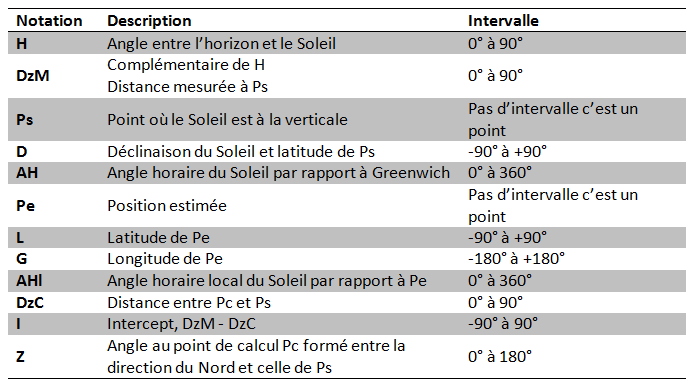
Avant de faire le calcul de DcZ et Z, on va récapituler les grandeur énoncées :

4. Calcul hardcore de DzC

Maintenant, passons aux calculs. On dispose d’une formule qui ressemble un peu à celle d’Al Kashi, mais qui ne vient pas d’Al Kashi donc laissons le tranquille chez les perses, pour obtenir DzC et Z.

Pour DzC :

\cos ⁡DzC =\cos⁡(90°-L) \cos⁡(90°-D) + \sin⁡(90°-L) \sin⁡(90°-D) \cos⁡ AHl

Ce qui se simplifie, avec des propriétés de trigo de base, en :

\cos ⁡DzC = \sin⁡ L \sin ⁡D + \cos⁡ L \cos⁡ D \cos⁡ AHl

\textcolor{red}{ DzC= \cos^{-1}⁡( \sin ⁡L \sin⁡ D + \cos ⁡L \cos ⁡D \cos ⁡AHl) } \:\:\:Equation(1)

5. Calcul hardcore de Z

Pour Z :

\cos⁡(90°-D)= \cos⁡(90°- L) \cos⁡DzC+sin⁡(90°- L) \sin⁡DzC \cos⁡Z

Ce qui se simplifie, avec des propriétés de trigo de base, en :

\sin D= \sin ⁡L \cos⁡ DzC + \cos ⁡L \sin⁡ DzC \cos⁡ Z
\cos⁡ L \sin⁡ DzC \cos ⁡Z= \sin ⁡D - \sin ⁡L \cos ⁡DzC
\cos ⁡Z = \frac{\sin⁡ D – \sin⁡ L \cos⁡ DzC }{ \cos⁡L \sin ⁡DzC }

\textcolor{red}{ Z=cos^{-1}⁡(\frac{\sin⁡D–\sin⁡L \cos⁡DzC }{\cos⁡L \sin⁡DzC })} \:\:\: Equation(2)

III. Un exemple avec calculs détaillés à la calculatrice

Maintenant que toute cette théorie a mis tout le monde dans le pâté et que tous ont décroché moins une fois, essayons nous à un exemple. Ça va utiliser ce qu’on a vu et permettre de comprendre avec des nombres.

Testons la méthode pour le jour du 11 mai 2020, parce que c’est surement la première activité en extérieur que vous ferez le jour du déconfinement. Même si toutes les courses ont été annulées cette année, on finit notre Mini Fastnet 2020 seul, sans concurrent, sans classement et surtout sans se soucier de la limite des 100km. Ça c’est de l’esprit Mini ! Le matin, en arrivant sous Ouessant, on s’embête un peu, il fait beau et on décide de faire une droite de hauteur.

A.Première droite de hauteur

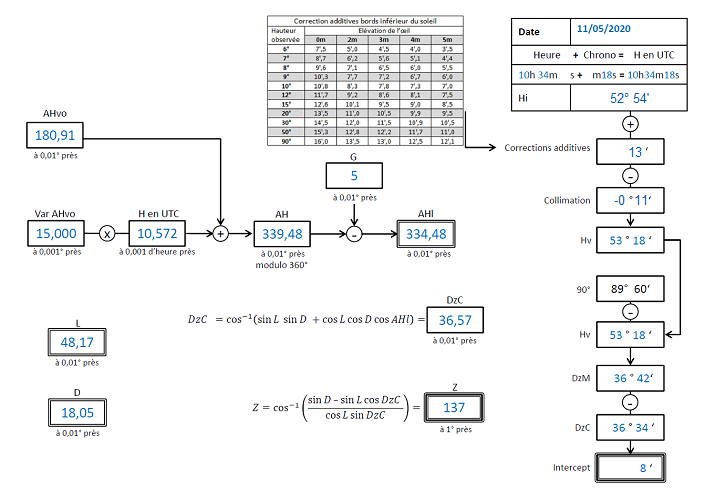
Le canevas de calcul complété :

Récupérer un canevas vierge

1. Mesure du sextant et du chrono

Toutes corrections faites sur notre mesure, on relève la hauteur du Soleil à 53°18′. Il était exactement 12H 34 et 18 secondes le 11/05/2020 à l’instant de la mesure.

2. Choix du point d’estime Pe

On choisit une position estimée avec pour seuls critères :

• Avec des coordonnées rondes
• Estimée sur notre carte

On fait le choix de Pe à 48°10’N et 5°W donc L =+ 48°10′ (positif car Nord) et G=+5° (positif car Ouest).

3. Distance zénithale mesurée DzM

Déjà, on peut calculer notre distance à la verticale du Soleil, Ps qui est 90°-H.

DzM=90°-H=90°-53°18'=36°42'\:

4. Position de Ps par les éphémérides (AH et D)

Regardons maintenant la position du pied du Soleil Ps à exactement 12H 34 et 18 secondes avec les éphémérides. On passe notre heure en UT soit 10H 34 et 18 secondes.

La longitude de Ps est AH qui aussi appelé angle horaire. La latitude de Ps est D qui aussi appelé déclinaison. On va calculer à l’aide des éphémérides AH et D.

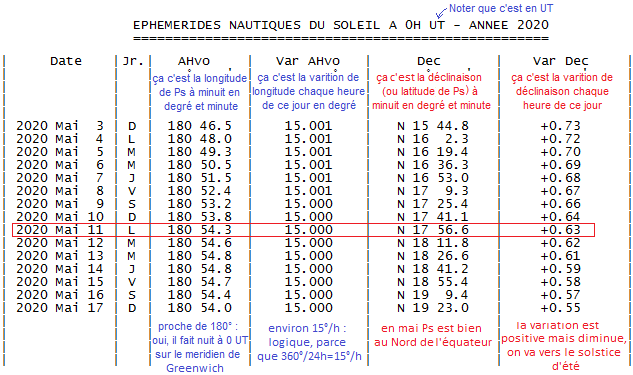
Pour les calculs on passera tout en degrés.

AH=AHvo+10h34'18"\times Var\,AHvo
AH=180°54,6'+ 10h34'18"\times 15,000°
AH= 180+\frac{54,6}{60}+(10+ \frac{34}{60} + \frac{18}{60 \times 60 })×15=180,91+10,572 \times 15
\fbox{AH = 339,48°}

Et pour la déclinaison D :

D=Dec+10,572 \times 0,63'\:
D=17°56,6'+10,571 \times 0,63'\:
D=17+\frac{56,6}{60}+10,571 \times \frac{0,63}{60}=17,94+10,571 \times 0,0105
\fbox{D=+18,05°}

5. Angle horaire locale AHl

On a choisi la position estimée Pe à 48°10’N et 5°W donc L =+ 48°10’ (positif car Nord) et G=+5° (positif car Ouest).

Calcul de l’angle horaire locale :

AHl=AH-G=339,48-5
\fbox{AHl=334,48°}

AHl est bien compris entre 0° et 360° donc c’est bon. On n’a pas besoin de lui soustraire ou ajouter 360° pour le ramener dans cet intervalle.

6. Distance zénithale calculée DzC

Calcul de DzC par l’équation 1 :

DzC = \cos^{-1} ⁡( \sin⁡L \sin⁡D + \cos⁡L \cos⁡D \cos⁡AHl )
DzC= \cos^{-1}⁡( \sin⁡ 48,17 \sin⁡18,05 + \cos⁡48,17 \cos⁡18,05 \cos⁡334,49 ) = 36,57°
\fbox{DcZ=36°34'\:}

On arrondit au mille près pour le résultat. La distance mesurée est plus grande que la distance calculée donc la position estimée est entre notre position et Ps.

I=DzM-DzC=36°42'-36°34'=8'\:
\fbox{I=8 milles}

7. Azimut Z de Ps depuis Pe

Calcul de Z par l’équation 2 :

Z= \cos^{-1}( \frac{\sin⁡D – \sin⁡L \cos⁡DzC }{ \cos⁡L \sin⁡DzC })

Z=cos^{-1}⁡( \frac{ \sin⁡18,05 – \sin⁡48,17 \cos⁡36,56 }{ \cos⁡48,17 \sin⁡36,56 })
\fbox{Z=137°}

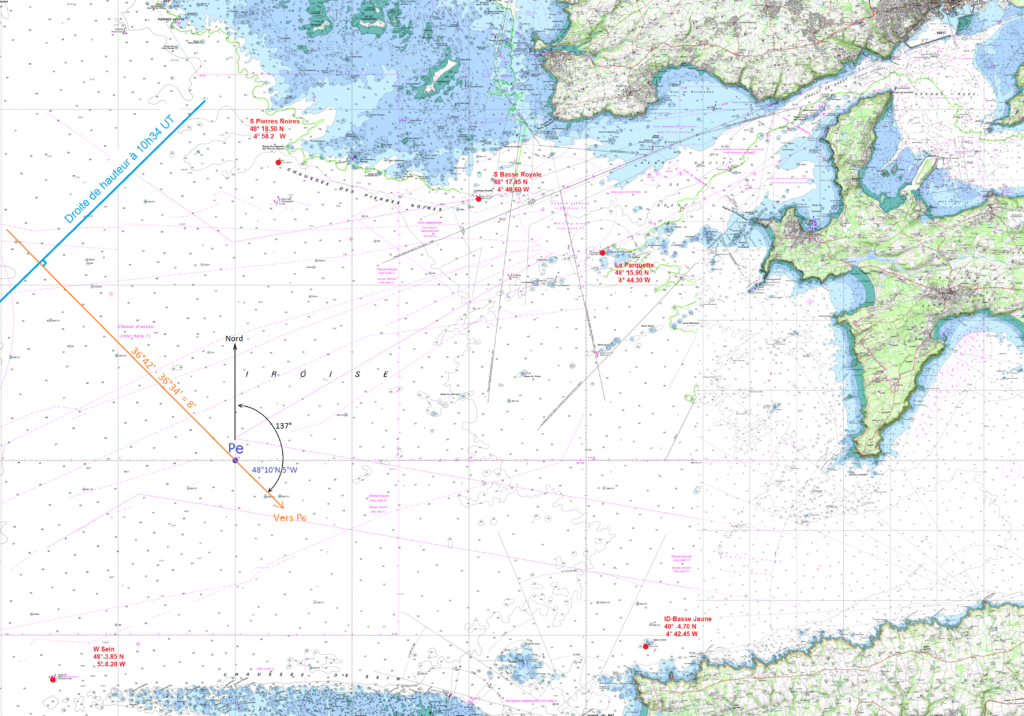
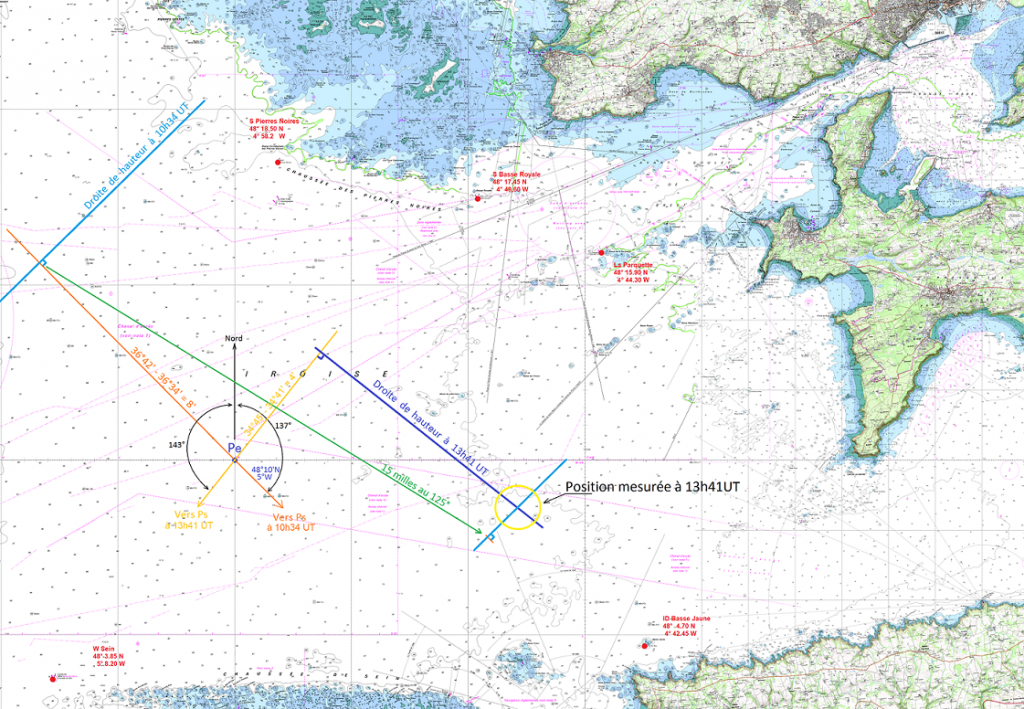
8. Tracé de la première droite de hauteur

On trace, en partant de Pe, la droite vers Ps d’angle 137° avec le Nord. L’intercept est positif donc on prolonge cette droite en s’éloignant de Ps à partir de Pe. Au bout de 8 milles on trace perpendiculairement la droite de hauteur.

Voir l’image en plus grand

B. Seconde droite de hauteur

Après avoir navigué peinard à 5 nœuds au 125° pendant 3 heures, on a encore soif de calcul barbant alors on refait une droite de hauteur.

On refait tous les calculs précédent mais je détaillerai moins…

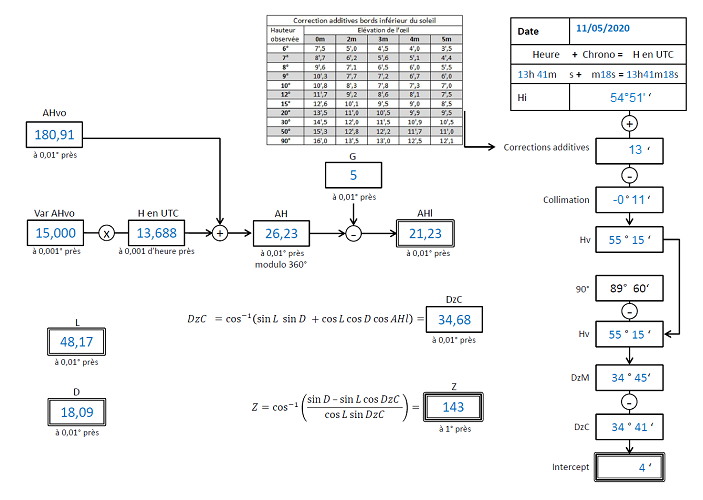
Le canevas de la deuxième droite complété :

1. Mesure du sextant et du chrono

Toutes corrections faites sur notre mesure, on relève la hauteur du Soleil à 55°15’ à exactement 15h41 et 18 secondes.

2. Choix de la position estimée Pe

On gardera la même position estimée soit Pe a pour coordonnées 48°10’N et 5°W donc L =+ 48°10’ (positif car Nord) et G=+5° (positif car Ouest).

3. Distance zénithale mesurée DzM

Déjà on passe la mesure de hauteur en distance à Ps :

DzM=90°-55°15'=34°45'\:
\fbox{DzM=34°45'\:}

4. Position de Ps par les éphémérides (AH et D)

On passe l’heure en UT et en décimale d’heure :

15h41'18 \: Heure\: d'été=13,688 h\: UT

Ensuite on s’occupe de l’angle horaire AH :

AH = 180,91+13,68 \times 15 = 386,23°

Ici AH est plus grand que 360° donc on lui soustrait 30° :

AH=386,39-360=26,23°

\fbox{AH=26,23°}

Maintenant calculons la déclinaison D :

D=17,94+13,688×0,0105 Nord donc positive

\fbox{D=18,09°}

5. Angle horaire locale AHl

On garde la même position estimée L=+48,17° et G=+5°. Calculons l’angle horaire locale AHl :

AHl=26,23°-5°

\fbox{AHl=21,23°}

6. Distance zénithale calculée DzC

Calcul de DzC par l’équation 1 :

DzC=\cos^{-1}⁡(\sin⁡48,17 \sin⁡18,09 + \cos⁡48,17 \cos⁡18,09 \cos⁡21,23 )=34,68°
\fbox{DzC=34,69°=34°41'\:}

La distance mesurée est plus grande que la distance calculée donc la position estimée est entre notre position et le pied du Soleil, Ps.

I=DzM-DzC=34°45'\:-34°41'\:=4'\:
\fbox{I=4 milles}

7. Azimut T de Ps depuis Pe

Calcul de Z par l’équation 2 :

Z=\cos^{-1}⁡(\frac{\sin⁡D–\sin⁡L \cos⁡DzC }{\cos⁡L \sin⁡DzC })

Z=\cos^{-1}⁡(\frac{\sin⁡18,09–\sin⁡48,17 \cos⁡34,68 }{\cos⁡48,17 \sin⁡34,68 })
\fbox{Z=143°}

L’angle horaire local AHl est compris entre 0° et 180° donc il s’agit de l’après-midi. L’angle Z sera donc tourné vers l’Ouest sur la carte.

8. Tracé de la seconde droite de hauteur

On trace, en partant de Pe, la droite vers Ps d’angle 143° avec le Nord. L’intercept est positif donc on prolonge cette droite de 4 milles en s’éloignant de Ps à partir de Pe. Au bout de 4 milles on trace perpendiculairement une nouvelle droite de hauteur.

Puis enfin on déplace la première droite de 3 heures à 5 nœuds soit de 15 milles au 125°.

Voir la carte en grand

Téléchargements

• Éphémérides
• Canevas de calcul